Canadian Science Letters X
Physics Tomorrow Canadian Science Letters X (CSX) An SCOPUS-indexed monthly thrice peer-reviewed journal. CSX journal is an international, peer-reviewed, partial open-access journal on theoretical, & applied science, science and its applications published monthly online by Physics Tomorrow Letters.
Indexing
Indexed within Scopus, SCIE (Web of Science), CAPlus / SciFinder, Inspec, and many other databases.
Open access
Free for readers, with article processing charges (APC) paid by authors or their institutions.

Rapid publication
Manuscripts are peer-reviewed and a first decision provided to authors approximately 21 days after submission; acceptance to publication is undertaken in 8-10 days post first decision.
Recognization
Reviewers who provide timely, thorough peer-review reports receive vouchers entitling them to a discount on the APC of their next publication in any Physics Tomorrow Letters, in appreciation of the work done.
Impact Factor
2.00 (based on last year record)
Journal Flyer
ISSN: 6987-9880
May 13, 2023
A method for automated regression test in scientific computing libraries: illustration with SPHinXsys
The development of computers has pushed scientific computing to become an indispensable part of many technologies and industries, such as in assessing climate change [2], designing new energy conductors [3], and imposes an ever-widening effect on better predicting and understanding the
phenomena of nature and engineered systems.
April 21, 2023
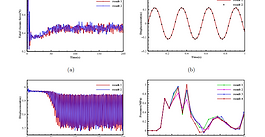
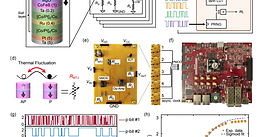
CMOS + stochastic nanomagnets: heterogeneous computers for probabilistic inference and
learning
Extending Moore’s law by augmenting complementary-metal-oxide semiconductor (CMOS) transistors with emerging nanotechnologies (X) has become increasingly important. Accelerating Monte Carlo algorithms that rely on random sampling with such CMOS+X technologies could have signicant impact on a large number of elds from probabilistic ........
April 21, 2023
Foundation of classical dynamical density functional theory: uniqueness of time-dependent density–potential mappings
When can we uniquely map the dynamic evolution of a classical density to a timedependent potential? In equilibrium, without time dependence, the one-body density uniquely specifies the external potential that is applied to the system.