

TOC (TphysicsLetters)
TOC (TphysicsLetters)
The Nature of the 1 MeV-Gamma Quantum in a Classic Interpretation of the Quantum
Nebular spectra from Type Ia supernov
TOC HIGHLIGHTS 2023
TOC HIGHLIGHTS 2023
Theoretical Physics Letters
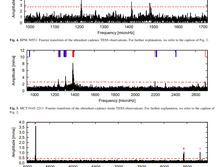
ZZ Ceti stars of the southern ecliptic hemisphere re-observed by TESS
ZZ Ceti stars of the southern ecliptic hemisphere re-observed by TESS





























